

(by R.R. Tucci, May 2006)
Once more unto the breach, dear friends, once more; Or close the wall up with our English dead! (from ``King Henry V" by W. Shakespeare)
Suppose you start with a 2-qubit circuit with 4 CNOTs. Find a way of expressing this circuit as another 4-CNOT circuit that has a gap in the bottom wire, between the two, middle CNOTs:
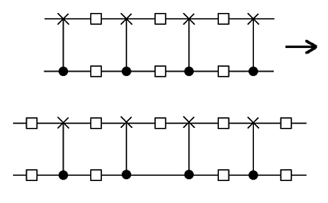
(In this figure, the horizontal arrow means ``can be expressed as", and the empty boxes stand for arbitrary 1-qubit gates). We will call this gap a ``breach", because we QC programmers are bards at heart. Aaah, the exquisite poesy of computer code! Now if you can open this breach, you already know how to close it. Yes, Indeedie. Now that there is a breach between them, these two middle CNOTs can be combined to form a single controlled-U. And this new controlled-U will have to its right (and to its left too) a CNOT, which is just a special case of a controlled-U. Recall that in Puzzler 1, you learned how to express a sequence of 2 controlled-Us as 2 CNOTs. Presto! you have reduced the original 4-CNOT circuit to a 3-CNOT circuit. And that's not all. Given a 2-qubit circuit with any number, greater than 3, of CNOTs, you can apply this technique repeatedly to reduce it to just 3 CNOTs. So, you clever scoundrel, you have found a neat way of reducing any 2-qubit circuit into a circuit with just 3 CNOTs. (Another way of doing this was invented by Vidal and Dawson; their way relies on 16-inch guns, viz, Cartan's KAK decomposition).