

(by R.R. Tucci, Sept 2005)
Thanks to an infamous 1995 paper with a cast of thousands, it is widely known that a single controlled-U gate can be expressed with just 2 CNOTs (and some 1-qubit gates); i.e.,
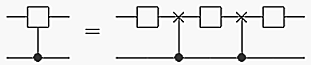
where the empty boxes represent 2-dimensional unitary matrices. But what happens if you have a circuit with two controlled-U gates? How many CNOTs are needed to express the circuit then? Show that any 2-qubit circuit with exactly two controlled-U's can be expressed with just 2 CNOTs (and some 1-qubit gates); i.e., show that

I like to call this a Deflation Identity, because the targets of the controlled-U gates are ``deflated" from boxes to x's; we pop them like balloons. It's possible to give a brief NON-CONSTRUCTIVE proof of this fact . That only gets you a grade of B. You are, after all, a highly respected QC Programmer, not a lousy, good for nothing, Theorist. To get an A, you need to find a CONSTRUCTIVE proof. If you can't solve it, ask your professor. If he or she can't solve it, get a better professor.