Qubiter

Copyright(c)1998-2007 R.R. Tucci. All rights reserved

News:

What is Qubiter?

Qubiter 1.11 is a free computer program pertaining to quantum computers (QC) and quantum Bayesian (QB) nets.

Currently, Qubiter is available only as pure C++ source code, without a graphical user interface.

In its current version 1.11, Qubiter takes as input an arbitrary unitary matrix, and returns as output an equivalent sequence of elementary operations (QC operations like controlled-nots and qubit rotations). Such sequences are often represented graphically by qubit circuits.

Future versions of Qubiter will take an arbitrary QB net as input, and return an equivalent sequence of elementary operations. We also plan to add further optimizations and some quantum error correction.

Some papers that will help you understand Qubiter:

Qubiter is brought to you courtesy of the Artiste company, makers of Quantum Fog. If you want to contribute to Qubiter, please contact us at

What is the connection between Quantum Fog and Qubiter?

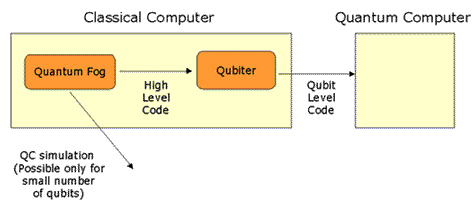
In classical computation, code is usually written in a high level language (such as C++), which, for the most part, does not mention bits. Then a compiler of some sort reduces the high level language to bit level instructions.

Quantum Fog is a tool for writing QC programs in a high level visual language, and then simulating the resulting programs. Quantum Fog can also feed this high level language to Qubiter. (The high level language uses decision diagrams called quantum Bayesian networks, which are discussed elsewhere in this website). Qubiter is a tool that translates this high level language to qubit level instructions which can then be fed to a QC. Hence we call Quantum Fog a quantum computer simulator and Qubiter a quantum compiler. Quantum Fog differs from other QC simulators presently available in that it is not a "bit level" simulator.

Where can I find Qubiter?

You may download Qubiter 1.11 source code by pressing here.(about 90 K).

Comments about Qubiter1.11 Distribution:

Qubiter 1.11 is fairly crude---a pure C++ program with no GUI. It's just a research tool, so don't expect too much. The Qubiter 1.11 distribution includes an XCode 2.4 project file. Qubiter is linked to the Clapack library.

XCode is an application (Integrated Development Environment) produced by Apple Inc. It provides an interface for the gcc (GNU) compiler. XCode is available for free at the Apple website.

Clapack is a library of linear algebra subroutines. It was produced by translating the Fortran library called Lapack into C via a tool called f2c. Clapack is available for free at www.netlib.org. Clapack is automatically included (as the vecLib Framework) in the standard installation of MacOS X .

Since Qubiter 1.11 is pure C++, you don't need XCode, or even Mac OS X to use it: you can run Qubiter on any platform for which you have a C++ compiler. However, if you don't use XCode, you will have to write your own makefile or project file. Furthermore, if you do not use MacOS X, you will have to install the Clapack library in your computer, if it isn't installed already, as it is in Macs.

General Linear Algebra Software:

Octave/Matlab Quantum Compiling Software:

CS Decomposition Corner:

Qubiter applies recursively a technique from Linear Algebra called the CS Decomposition (CS = Cosine Sine). The CS decomposition is very closely related to the Generalized Singular Value Decomposition (GSVD). To perform the CS decomposition, Qubiter calls subroutines from Clapack, a free software package available at Netlib. The Matlab software package (sold by The Mathworks) also contains subroutines that can do the CS decomposition.

Here are some authors of papers and/or software dealing with the CS decomposition:

Related Papers:

Caveat Emptor:

Scientists have a deep moral obligation to cite all important prior art in their scientific papers. Some individuals have studiously avoided citing the paper "A Rudimentary Quantum Compiler" in their papers about quantum compilers, even though Qubiter preceded their work by several years. I cite the work of these individuals in this web page, because I choose not to sink to their level, but this should not be construed as my endorsement of their character. I believe that honest competition is highly beneficial to science, and I encourage it. But hiding prior art is not honest competition. It is unethical, sleazy behavior that damages the scientific community in many ways.

Other Groups That Have Worked in the Past on Quantum Compiling:

(in alphabetical order)

[Home Page]