

(by R.R. Tucci, May 2006)
Our Puzzlers so far have dealt exclusively with 2-qubit circuits. Clearly, our puzzler diet is deficient in some essential multi-qubits. Here is a tasty morsel of 3-qubit circuits to supplement our diet. Suppose you have two CNOTs acting on 3 qubits. Suppose that the two CNOTs have the same target qubit but different control qubits. When can we ``pass one CNOT through the other"? Pictorially, when can we do this:
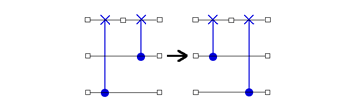 (1)
(1)
(In the above figure, the horizontal arrow means ``can be expressed as", and the empty boxes stand for arbitrary 1-qubit gates.) Clearly, the transformation Eq.(1) may come in handy if the shortie CNOT, by jumping over the tall CNOT, can find 3 other shortie CNOTs waiting for him on the other side; for then these 4 shortie CNOTs can be merged into just 3 shorties. It's as if a plump, shortie sheep wanted to jump over a tall fence to reach greener pastures on the other side.
So, intrepid QC Programmer, your goal is to find simple-to-check necessary and sufficient conditions under which Eq.(1) is possible. And, it goes without saying, only if you produce a CONSTRUCTIVE proof will you earn the respect of your fellow programmers.
Aah, QC Programmer, as no doubt you have anticipated, the circumstances under which Eq.(1) is possible are fairly limited. But what if, instead of starting alone, shortie started off as part of a small flock of shortie CNOTs on the right-hand-side of the tall CNOT. Could the flock propel one of their own over the wall? What we have in mind is this:
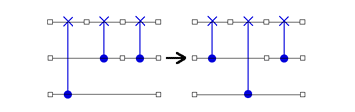 (2)
(2)
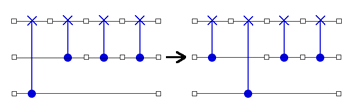 (3)
(3)
Your next goal, courageous QC Programmer, is to find necessary and sufficient conditions (and a construction) under which Eq.(2) is possible. And to do likewise for Eq.(3).